घन करने के आसान तरीके
घन करने का अर्थ किसी दी हुई संख्या को आपस में तीन बार गुणा करना है. यदि आपसे यह कहा जाये की आप 2 का घन निकाले तो आपको 2 को आपस में तीन बार गुणा करना पड़ेगा; इसी तरह 3 का घन निकालने के लिए आप 3× 3× 3 = 27 करेंगे
यदि आपको 2 या 3 अंक की किसी संख्या का घन निकालने के लिए कहा जाये तो आप जो मौजूदा तरीके अपनाएंगे वह काफी उबाऊ और समय बर्बाद करने वाला होगा परन्तु हम यहाँ जिन विधियों की चर्चा करेंगे वो काफी आसान, कम उबाऊ और आपके समय को बचाने वाला होगा लेकिन इसके लिए आपको पहले 10 संख्याओं का योग करना पड़ेगा. आपकी सुविधा के लिए यहाँ पहले 10 संख्या का घन दिया गया है
संख्या 1 2 3 4 5 6 7 8 9 10
घन 1 8 27 64 125 216 343 512 729 1000
इस तालिका को याद रखने के बाद आपको तीव्र गणना करने में मदद मिलेगी. चलिए हम सबसे पहले घन करने की सबसे आसान विधि के बारे में जानें. शुरू करने से पहले आपसे अनुरोध करूँगा की आप सबसे पहले गुणा करने की कुछ विधि को जो इस पुस्तक में दी गयी है को दुबारा आत्मसात कर ले और सबसे महत्वपूर्ण बात की आपको दो लगातार संख्या का तीव्र गुणन करना आना चाहिए.
क्या आप नए विधि को जानने के लिए उत्सुक हैं. तो आइये बिना समय गवाएं हम इस नयी विधि को सीखें. आप जानते हैं की -
a^3 = a^3 – a + a
= a (a^2 – 1) + a
= (a – 1) × a × (a+1) + a
उपरोक्त उदाहरणों से यह स्पष्ट हो जाता है की आपको तीन संख्या का गुणा करना आना आवश्यक है तभी आप तीव्रता से घन कर पाएंगे. मैंने इसी पुस्तक में तीन लगातार संख्या को गुणा करने की विधि की बात की है.
उदाहरण:- 11 का घन बताएं
हल:- यहाँ a = 11 है अतः इसके पूर्ववत और अगली संख्या क्रमशः 10 और 12 होंगे. सबसे पहले आप 10 , 11 एवं 12 को गुणा करें और परिणाम में 11 जोड़ दें.
उदाहरण:- 25 का घन बताएं
हल:- यहाँ a = 25 है अतः इसके पूर्ववत और अगली संख्या क्रमशः 24 और 26 होंगे. सबसे पहले आप 24 , 25 एवं 26 को गुणा करें और परिणाम में 25 जोड़ दें.
उदाहरण:- 99 का घन बताएं
हल:- यहाँ a = 99 है अतः इसके पूर्ववत और अगली संख्या क्रमशः 98 और 100 होंगे. अतः सबसे पहले आप 98 , 99 एवं 100 को गुणा करें और परिणाम में 99 जोड़ दें. किसी संख्या को 100 से गुणा करने के लिए आपको परेशानी नहीं होगी.
डॉ राजेश कुमार ठाकुर
rkthakur1974@gmail.com
Subscribe to:
Post Comments (Atom)
बारिश में अधिक कौन भीगेगा
क्या आप जानते हैं – अली नेसिन को टर्की में गणित ग्राम की स्थापना और गणित के प्रचार -प्रसार के लिए 2018 में लीलावती पुरस्कार प्रदान किया ...

-
वैदिक गणित मित्रों , वैदिक गणित 16 सूत्रों और 16 उपसुत्रों पर आधारित एक ऐसी प्रणाली है जिसमे अंकगणित , बीजगणित , नियामक ज्यामिति ,...
-
लघुत्तम और महत्तम समापवर्तक जैसा की आपको पता है कि प्रतियोगी परीक्षा में इस अध्याय से 1-2 प्रश्न अवश्य ही पूछे जाते है इसलिए यह अनिवार्य ह...
-
दो परिमेय संख्या के बीच अनगिनत परिमेय संख्या निकालना:- यदि दो संख्या p और q हैं और इनके बीच हमें n परिमेय संख्या निकालना है तो इसके द...

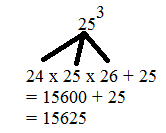



10kaghan
ReplyDelete