बहुभुज के अन्तःकोणों का योग कैसे निकालें

 

बहुभुज में सबसे छोटी ईकाई त्रिभुज है जिसके सभी कोणों का योग 180 अंश होता है. यदि इसे आधार मान लिया जाये तो बहुभुज के सभी कोणों का योग (n – 2) ×180 अंश क्यों होता है?

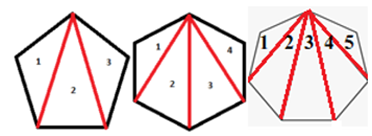
एक बहुभुज कि कल्पना कीजिये जिसकी ‘n’ भुजा है. जैसा कि आप जानते हैं कि n भुजा वाले बहुभुज के अंदर n त्रिभुज होंगे. यदि एक अष्टभुज कि बात कि जाये तो इसके अंदर आठ त्रिभुज बनेंगे जैसा चित्र में दिखाया गया है.

चूँकिएक त्रिभुज के सभी कोणों का मान 180 अंश होता है इसलिए n त्रिभुजों के लिए आंतरिक कोण 180 × n होगा.

बहुभुज के सभी आंतरिक कोणों का योग + केंद्र O पर बने सभी कोणों का योग = 180× n होगा ---- (1)

केंद्र O पर बने कोणों का योग = 360 अंश --- (2)

 समीकरण (1) में समीकरण (2) का मान रखने पर हम पाते हैं कि –                    

 बहुभुज के सभी आंतरिक कोणों का योग +360  = 180× n

अतः बहुभुज के सभी आंतरिक कोणों का योग = 180 n – 360 = 180(n -  2)

इसे आप किसी भी बहुभुज के आन्तरिक कोणों का योग ज्ञात करने के लिए प्रयोग कर सकते हैं. ध्यान रहे किसी भी सामान्य बहुभुज जिसकी ‘n’ भुजा है को n – 3 विकर्ण द्वारा n – 2 त्रिभुजों में बाँट सकते हैं. अतः बहुभुज के सभी अन्तः कोणों का योग (n-2) × 180 के बराबर होता है.

दिए गये चित्र में यह स्पष्ट दिख रहा है कि n भुजा वाले बहुभुजों में त्रिभुजों की संख्या कुल भुजाओं कि संख्या से 2 कम होता है.

 इतिहास के झरोखे से – जैसे- जैसे बहुभुज कि भुजाओं कि संख्या बढती जाएगी उसका आकर वृत्त के करीब आता जायेगा.

यहाँ ऊपर कि ओर बने चित्र 1699 के हैं जिसमे एक पट्टी के भीतर n के मान 3 से 12 तक कि आकृति बनी हुई है. बहुभुज के प्रयोग के बारे में कहा नहीं जा सकता है परन्तु पाइथागोरस के स्कूल में पढने वाले सभी छात्रों के लिए पेंटाग्राम  (पञ्चसितारा) का प्रयोग दिखता है. सातवीं शदी ईसा पूर्व में एरिस्टोफ़नीज ने सितारे के आकार का बहुभुज का प्रयोग एक विशालकाय बर्तन के उपर नक्काशी के रूप में किया है. आर्कमिडीज ने 5 भुजा वाले बहुभुज से 92 भुजा वाले बहुभुज के अंदर और बाहर वृत्त कि संरचना कर पाई का मान निकालने में सफलता प्राप्त की.  बहुभुज जिसे अंग्रेजी में polygon कहते हैं की उत्पति polus – अनेक , अधिक और gonia – कोना या कोण से हुई है. आइये कुछेक बहुभुजों के नाम जानते हैं- 

भुजा	नाम	भुजा	नाम	भुजा	नाम
30	ट्रायेकोंटागन	40	टेट्राकोंटागन	50	पेंटाकोंटागन
100	हेक्टोगन	1000	चिलियागन	10000	मेरियागन
1000000	मेगागन	1,000,000,000,000,000,000,000,000	योटागन	अनंत भुजाये	अपिरोगन

जहाँ तक बहुभुजो के कोण का सवाल है इसे आसानी से उपरोक्त सूत्र द्वारा निकाला जा सकता है- 

बहुभुज	अन्तःकोण	बहुभुज	अन्तः कोण	बहुभुज	अन्तःकोण
त्रिभुज	180	चतुर्भुज	360	पंचभुज	540
षट्भुज	720	सप्तभुज	900	अष्टभुज	1080

बहुभुज के बाहरीकोण का योग हमेशा 360 अंश का होता है. इसलिए नियमित बहुभुज के प्रत्येक अन्तःकोण या बाहरी कोण का मान अन्तः कोण या बाहरी कोण के मान को भुजा कि संख्या से भाग देकर प्राप्त किया जा सकता है.