ब्रह्मगुप्त का चक्रीय चतुर्भुज

 

क्या आप जानते हैं ?

गणित के इतिहास में अगर महत्वपूर्ण भारतीय गणितज्ञ की बात की जाए तो  ब्रह्मगुप्त का स्थान निसंदेह काफी ऊँचा माना जा सकता है. इन्होने ना केवल शून्य को परिभाषित कर इससे सम्बंधित नियमों का प्रतिपादन किया बल्कि आज हम जो भी गणितीय संक्रिया जमा , घटा, गुणा और भाग की बात करते हैं उसके बारे में विश्व को इन्हीं के पुस्तक ब्रह्मस्फुटसिद्धांत से पता चलता है. अंकगणित , बीजगणित ही नहीं ज्यामिति में भी इन्होने काफी योगदान दिया. 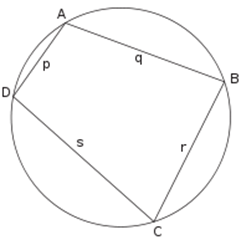सबसे मजेदार तो चक्रीय चतुर्भुज का क्षेत्रफल निकालने सम्बन्धी सूत्र है. इन सूत्रों में आसन्न और पूर्ण क्षेत्रफल निकालने का भी उल्लेख मिलता है.

                     

 

 

 

 

 

 

 

यदि किसी चक्रीय चतुर्भुज की भुजाएं p, q, r एवं s हों तो आसन्न क्षेत्रफल इनके विपरीत भुजाओं के योग के आधे का  गुणनफल होता है. अर्थात आसन्न क्षेत्रफल =  होगा तथा वास्तविक  क्षेत्रफल के लिए सबसे पहले अर्धपरिमाप निकालने की जरूरत पड़ेगी जो    होगी और इसका क्षेत्रफल  होगा . ऐसे देखने  में यह हीरोन सूत्र के समान है पर  ब्रह्मगुप्त ही वो गणितज्ञ थे जिन्होंने इसपर सर्वप्रथम विचार किया. जिष्णुगुप्त के पुत्र ब्रह्मगुप्त का जन्म 598 इसवी में हुआ था और इन्होने राजस्थान के भीनमाल जगह में जीवन का बहुमूल्य समय बिताया.

अब दुसरे लोकप्रिय गणितग्य की बात करें तो फिबोनिकी का स्थान भी   विश्वपटल में काफी बड़ा है.  भारतीय गणितीय अंक जिसमे 0 से लेकर 9 तक के अंक हैं को पुरे यूरोप में पहुँचाने का काम इन्होने ही किया. 1220 में लिखी अपनी पुस्तक लिबर अबच्ची (liber abacci) या अंको की पुस्तक में इन्होने भारतीय अंको के बारे में पुरे यूरोप को बताया. इनकी श्रृंखला जिसमे प्रत्येक अगला अंक पिछले दो अंको के योग के बराबर होता है जैसे – 1, 1, 2, 3, 5, 8, 13, 21, 34 ,--- को ऐसे तो भारत में 400 वर्ष पूर्व ही खोज ली गयी थी परन्तु जैन गणितज्ञ हेमचन्द्र को इसका श्रेय काफी देर से मिला. फिबोनिकी ने इसी तरह  ब्रह्मगुप्त के खोजे गये संख्या सूत्र  को अपनी पुस्तक में स्थान दिया और वो संख्या फिबोनिकी के नाम से जाना गया. बाद में इस संख्या सूत्र जिसका विवरण नीचे है को फिबोनिकी –ब्रह्मगुप्त के संयुक्त नाम से जाना जाने लगा. ब्रह्मगुप्त ने दो संख्याओं के वर्गों के योग के गुणनफल को दो तरीके से लिखने में सफलता पाई

उदाहरण के लिए

ऐसे तो यह तादात्म्य सबसे पहले डायोफैंटस ने अपनी पुस्तक अरिथमेटिका में तीसरी सदी में उल्लेख किया परन्तु इसे दुबारा स्थापित करने का श्रेय ब्रह्मगुप्त को जाता है. उन्होंने अपनी पुस्तक ब्रह्मस्फुटसिद्धांत में इसका उल्लेख किया है. मोहम्मद अल फाजिरी ने जब इस पुस्तक का संस्कृत से अरबी में अनुबाद किया और फिर अरबी से फिबोनिकी ने अपनी पुस्तक वर्गों की पुस्तक (BOOK OF SQUARES) में लैटिन में अनुवाद किया तो इस तादात्म्य का उल्लेख करना नहीं भूले.

डायोफैंटस ने अपनी पुस्तक अरिथमेटिका में एक अन्य प्रमेय का जिक्र किया है. उनके अनुसार प्रत्येक धन संख्या को चार संख्याओं के वर्गों के योग के रूप में लिखा जा सकता है. ऐसे इसका व्यावहारिक प्रमाण फरमा ने सबसे पहले दिया पर वो इसे प्रकाशित नहीं करवा पाए और इस प्रमेय को दुबारा लेग्रेंज ने सत्यापित किया और आज इसे लेग्रेंज के चार वर्गों का प्रमेय के रूप में जानते हैं.

23 = 1² + 2² + 3² + 3²

कुछेक संख्या को अलग अलग तरीके से इसी प्रमेय की मदद से लिखा जा सकता हैं. मसलन 31O को यहाँ चार अलग प्रकार से लिखा गया है.

इतालियन गणितज्ञ लेग्रेंज को न्यूटन की तरह कैलकुलस के खोज के लिए जाना जाता हैं. इंटरनेशनल कांग्रेस ओन इंडस्ट्रियल एंड एप्लाइड मैथमेटिक्स द्वारा 1999 से लगातार हर चार वर्ष के अन्तराल पर लाग्रांज पुरस्कार दिया जाता है.

डॉ राजेश कुमार ठाकुर